PARCIAL 2
MODELO ALGEBRAICO GENERAL DE FUNCIONES POLINOMIALES
FUNCIONES CUADRÁTICAS
MODELO GRÁFICO

La gráfica de una ecuación cuadrática es muy útil para identificar cuántas soluciones y qué tipos de soluciones tiene una función. Hay tres diferentes situaciones que ocurren cuando se gráfica una función cuadrática.
Factorizando la expresión obtenemos
x = x + 5 x - 2
Las raíces de la función x = x 2 + 3 x - 10 son x=5 y x=-2
Puedes visualizar estas raíces observando la gráfica de esta función, que es la siguiente:

| o |
Puedes visualizar estas raíces observando la gráfica de esta función, que es la siguiente:

| Si una función cuadrática tiene dos raíces reales su fórmula se puede escribir en la forma k(x-a)(x-b) donde a y b son números reales. En este caso, la gráfica atraviesa el eje x dos veces. |
|---|
Ahora bien, el discriminante, precisamente es una parte de esta fórmula, pero una parte realmente muy importante ya que nos permitirá (si lo estudiamos por separado) determinar cuántas y qué tipo de soluciones tendrá la ecuación cuadrática en cuestión. De allí su nombre…, porque si lo piensas lo que nos permite en definitiva es discriminar.
Pero vamos por partes… ¿a qué parte de esta fórmula llamamos exactamente discriminante? La siguiente imagen te lo muestra claramente:
Se llama discriminante a la parte que está afectada por la raíz cuadrada, que, en la imagen anterior está destacada en color rojo.
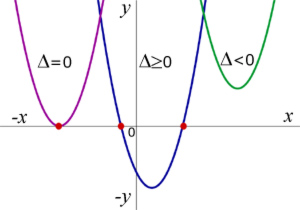
¿Para qué nos sirve analizar el discriminante? Porque de su análisis sólo podrán surgir tres casos y en consecuencia, habrá sólo tres tipos de raíces o soluciones. El detalle consta en la siguiente imagen:
El discriminante se simboliza con la letra griega Delta, por lo que con frecuencia encontrarás expresiones como la que sigue, cuando se hace referencia al estudio de un discriminante:

Esto mismo, expresado desde el punto de vista de la gráfica de la ecuación cuadrática (es decir cuando se convierte en función), se visualiza mucho mejor; presta atención
Forma estándar de una función cuadrática
La forma estándar de una ecuación cuadrática es y = ax^2 + bx + c, donde a, b y c son coeficientes y la y y la x son variables. Es más fácil resolver una ecuación cuadrática cuando está en su forma estándar ya que puedes computar la solución con a, b y c. De todos modos, si necesitas graficar la función cuadrática, o parábola, el proceso es más simple cuando la ecuación está en la forma canónica. Esta es de la forma: y = m(x-h)^2 + k.
Pasos para convertir una función cuadrática en su forma general a estándar:
Forma factorizada
  
Toda función cuadrática se puede factorizar en función de sus raíces. Dada:
se puede factorizar como:
siendo a el coeficiente principal de la función, por ello se extrae siempre como factor común, de no escribirse, el coeficiente de x2 sería siempre 1. x1 y x2 representan las raíces de f(x). En el caso de que el Discriminante Δ sea igual a 0 entonces x1 = x2 por lo que podríamos escribir:
En este caso a x1 se la denomina raíz doble, ya que su orden de multiplicidad es 2.
FUNCIONES DE GRADO SUPERIOR
MODELO GRÁFICO
La función polinomial de tercer grado más sencilla es:
Grafícala, encuentra sus raíces, dominio y contradominio.
Empezamos calculando sus raíces. Para que
Para encontrar el dominio recuerda que el dominio de cualquier función polinomial es el conjunto de los números reales. El contradominio se calcula de la sigiuente manera:
Entonces, el contradominio también es el conjunto de los números reales, porque cuando

Observa que la función
Para encontrar una raíz de la función debemos contestar a la pregunta: ¿Qué número multiplicado por sí mismo tres veces es igual a cero? Y la respuesta es obvia: el número cero multiplicado por sí mismo nos da cero,
RAÍCES: TEOREMA DEL RESIDUO, DEL FACTOR Y DIVISIÓN SINTÉTICA
Entre tantas operaciones algebraicas encontramos la división de polinomios . Y, entre ellas, tenemos el caso específico de dividir un polinomio entre un binomio .
Cuando un polinomio es dividido entre un binomio, generalmente hay un residuo.
Y el teorema del residuo establece que si un polinomio de x, f(x) , se divide entre (x – a) , donde a es cualquier número real o complejo, entonces el residuo es f(a) .
Esto significa que para encontrar el residuo cuando un polinomio es dividido entre un binomio el valor de x es igual al valor a, o f(x) = f(a) .
En estos casos, debemos calcular entonces el valor de x, que será igual al de a.
Considere el polinomio x 2 – 8 x + 6 , el cual podemos identificar como una función polinomial f( x ) = x 2 – 8 x + 6 .
|
Dividamos este polinomio entre el binomio x – 2 , para ver si hay un residuo:
Podemos realizar la división en cualquier método.
Método 1: División larga
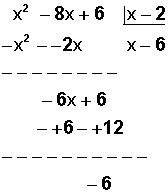
El residuo es -6
TEOREMA DEL FACTOR
Si a es una raíz de ƒ(x), entonces x - a es un factor del polinomio, donde a es un número real.
Aquí podemos observar la importancia de conocer el valor del residuo, ya que si éste es igual a cero, nos va a indicar que hemos encontrado un factor del polinomio y con él, una raíz del polinomio (una solución a la ecuación polinomial ƒ(x) = 0).
Aquí podemos observar la importancia de conocer el valor del residuo, ya que si éste es igual a cero, nos va a indicar que hemos encontrado un factor del polinomio y con él, una raíz del polinomio (una solución a la ecuación polinomial ƒ(x) = 0).
Función Racional
En matemáticas, una función racional de una variable es una función que puede ser expresada de la forma:
donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo, esta fracción es irreducible, es decir que las ecuaciones P(x) = 0 y Q(x) = 0 carecen de raíces comunes. Esta definición puede extenderse a un número finito pero arbitrario de variables, usando polinomios de varias variables.
La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.
Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados de otras funciones más complejas, ya que son computacionalmente simples de calcular como los polinomios, pero permiten expresar una mayor variedad de comportamientos.
Ejemplos
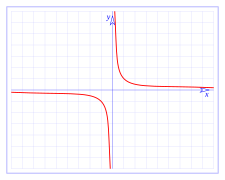
si el denominador es distinto de cero, y si ad ≠ bc, la curva correspondiente es una hipérbola equilátera.1
Propiedades
- Toda función racional es de clase en un dominio que no incluya las raíces del polinomio Q(x).
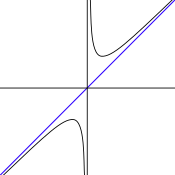
- Todas las funciones racionales en las que el grado de Q sea mayor o igual que el grado de P tienen asíntotas (verticales, horizontales u oblicuas).
- Todas las funciones racionales cuyos coeficientes pertenecen a un cuerpo forman un cuerpo que incluye al cuerpo base como subcuerpo. El cuerpo de funciones racionales forma un subcuerpo del cuerpo de series de potencias formales.
Integración de funciones racionales
Dada una función racional:
Si el denominador es un polinómico mónico con k raíces diferentes, entonces admitirá la siguiente factorización en términos de polinomio irreducibles:
Si entonces la función racional puede escribirse como combinación lineal de fracciones racionales de las formas:
Por lo que la integral de la función es una combinación lineal de funciones de la forma :
Obsérvese que lo anterior implica que las funciones racionales constituyen un cuerpo algebraico que es cerrado bajo la derivación, pero no bajo la integración.

Asíntota
En matemática, se le llama asíntota de la gráfica de una función a una recta a la que se aproxima continuamente la gráfica de tal función;1 es decir que la distancia entre las dos tiende a ser cero (0), a medida que se extienden indefinidamente.
O que ambas presentan un comportamiento asintótico. Generalmente, las funciones racionales tienen comportamiento asintótico.
O que ambas presentan un comportamiento asintótico. Generalmente, las funciones racionales tienen comportamiento asintótico.
Las asíntotas ayudan a la representación de curvas, proporcionan un soporte estructural e indican su comportamiento a largo plazo. En tanto que líneas rectas, la ecuación de una asíntota es simplemente la de una recta, y su expresión analítica dependerá de la elección del sistema de referencias (y = m•x + b en coordenadas cartesianas).
Si bien suelen representarse en un mismo sistema de coordenadas, las asíntotas no forman parte de la expresión analítica de la función, por lo que -en numerosos ejemplos- no están incluidas explícitamente dentro de la gráfica, o bien se las indica con una línea punteada.
En muchos casos, las asíntotas coinciden con los ejes de coordenadas, es decir que sus ecuaciones en coordenadas cartesianas serán: x = 0, y = 0.
En muchos casos, las asíntotas coinciden con los ejes de coordenadas, es decir que sus ecuaciones en coordenadas cartesianas serán: x = 0, y = 0.
Se distinguen tres tipos:
- Asíntotas verticales: rectas perpendiculares al eje de las abscisas, de ecuación x = constante.
- Asíntotas horizontales: rectas perpendiculares al eje de las ordenadas, de ecuación y = constante.
- Asíntotas oblicuas: si no son paralelas o perpendiculares a los ejes, de ecuación y = m•x + b.

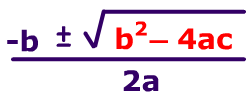





![f(x)={\frac {P(x)}{Q(x)}},\qquad P(x),Q(x)\in \mathbb{R} [x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4e816041f96755f2f06f265331e8ee88d14b407)









Comentarios
Publicar un comentario