La gráfica de una
función cuadrática es una parábola. Pero el concepto geométrico de parábola es más amplio, como veremos a continuación.
El siguiente gráfico muestra una “parábola acostada”:
Existen también las parábolas rotadas. Por ejemplo si nosotros graficáramos en algún
programa de computadora el conjunto de puntos que satisfacen la ecuación
x2+2xy+y2+2x–2y=0, obtendríamos la siguiente gráfica:
Definición de parábola
Dados un punto F (foco) y una recta r (directriz), se denomina parábola al conjunto de puntos del plano que equidistan del foco y de la directriz.
Simbólicamente:
P={P(x,y)|d(P,r)=d(P,F)}
Observen que estamos definiendo la parábola como un conjunto de puntos que verifican cierta propiedad geométrica, no como la gráfica de una función cuadrática (que es como ustedes la conocían hasta ahora).
El eje focal es el eje perpendicular a la directriz que pasa por el foco. Es el eje de simetría de la parábola.
El punto de la parábola que pertenece al eje focal se llama vértice.
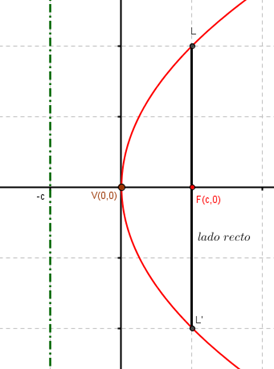
Para el esquema que realizamos, las coordenadas del vértice son V(0,0), las del foco F(c,0) y la recta directriz está dada por r:x=–c. Las coordenadas de un punto genérico Q que pertenece a la directriz son (–c,y).
Ahora con estos datos vamos a deducir la ecuación. Por definición:
d(P,r)=d(P,F)
Distancia entre un punto P y la directriz:
Distancia entre un punto P y el foco:
Las igualamos según lo establece la definición:
Donde los vectores y sus módulos son:
−−→PQ=(–c–x,0)
−−→PF=(c–x,–y)
Ahora sustituyendo y operando llegamos a:
√c2+2cx+x2=√c2–2cx+x2+y2
c2+2cx+x2=c2–2cx+x2+y2
y2=4cx(c≠0)
Que es la ecuación canónica de la parábola con V(0,0) y eje focal y=0 (eje x).
Donde si,
c>0⇒ Las ramas de la parábola apuntan hacia la derecha
c<0⇒ Las ramas de la parábola apuntan hacia la izquierda
Análogamente a lo desarrollado para una parábola con eje focal horizontal, se puede hacer la deducción para las parábolas con eje focal vertical. Si permutamos variables sobre la expresión canónica tenemos la expresión canónica de la parábola vertical:
x2=4cy
Ecuación canónica de la parábola con V(0,0) y eje focal x=0 (eje y).
Donde si,
c>0⇒ Las ramas de la parábola apuntan hacia la arriba
c<0⇒ Las ramas de la parábola apuntan hacia la abajo
Coordenadas del foco: F(0,c)
Ecuación de la directriz d:y=–c
Ecuación ordinaria de la parábola
Consideremos una parábola cuyo vértice V(α,β) no coincide con el origen del sistema xy :
¿Cómo sería la ecuación de la parábola en el sistema de referencia xy? No sabemos responder esto por el momento. Pero si armamos un nuevo sistema cuyo centro coincida con V, la ecuación canónica en este nuevo sistema sería:
y′2=4cx′
Debemos realizar una traslación de ejes para poder tener la ecuación escrita en el sistema xy
¿Qué coordenadas tiene el punto P respecto de cada sistema?
El punto es el mismo pero estamos modificando el sistema de referencia:
- Coordenadas de P en sistema x′y′
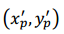
- Coordenadas de P en sistema xy
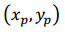
La relación entre los dos sistemas de coordenadas es la siguiente:
x′+α=x
y′+β=y
O reordenando:
{x′=x–αy′=y–β
Éstas son las ecuaciones de traslación de ejes.
Si reemplazamos las ecuaciones de traslación en la expresión y‘2=4cx′ obtenemos la ecuación en el sistema original:
(y–β)2=4c(x–α)
Ésta es la ecuación ordinaria de la parábola con vértice V(α,β) y eje focal paralelo al eje x.
Análogamente:
(x–α)2=4c(y–β)
Es la ecuación de la parábola con vértice V(α,β) y eje focal paralelo al eje y.
¿Cómo nos damos cuenta si el eje focal es vertical u horizontal? Observando cuál de las variables está elevada al cuadrado:
- Si y está al cuadrado, entonces es horizontal.
- Si x está al cuadrado, entonces es vertical.
Ejemplo
Hallar la ecuación de la parábola de directriz x=4 y foco F(–2,0).
Resolución
Es conveniente realizar una figura de análisis que represente los datos del enunciado:
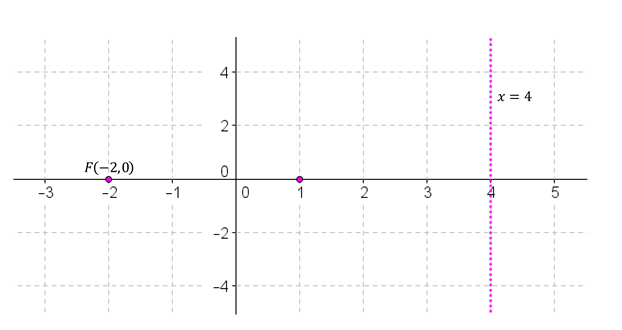
El valor absoluto de c es la distancia del vértice al foco.
|c|=d(V,F)
El vértice está sobre el eje focal y a la misma distancia del foco que de la directriz:
V=(–2+42,0)=(1,0)
Eje focal: eje x
Como el eje es horizontal la ecuación tiene la forma:
(y–β)2=4c(x–α)
(y–0)2=4c(x–1)
Falta calcular el valor absoluto de c.
|c|=d(F,V)=3
Como el foco está a la izquierda del vértice entonces c=–3.
Entonces queda:
y2=–12(x–1)
Lado recto
El lado recto es la longitud de la cuerda que es perpendicular al eje focal y pasa por el foco. Se puede demostrar que la longitud del lado recto es |4c|
∣∣LL′∣∣=|4c|
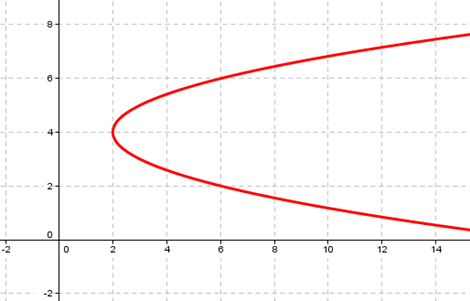 Existen también las parábolas rotadas. Por ejemplo si nosotros graficáramos en algún programa de computadora el conjunto de puntos que satisfacen la ecuación , obtendríamos la siguiente gráfica:
Existen también las parábolas rotadas. Por ejemplo si nosotros graficáramos en algún programa de computadora el conjunto de puntos que satisfacen la ecuación , obtendríamos la siguiente gráfica: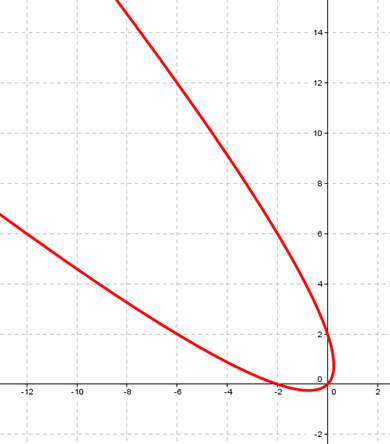 Para reconocer que esa gráfica efectivamente responde a la definición, características y expresión analítica de una parábola, debemos usar autovalores y autovectores. (Esto lo veremos más adelante en la Unidad 8: Aplicaciones de la diagonalización)
Para reconocer que esa gráfica efectivamente responde a la definición, características y expresión analítica de una parábola, debemos usar autovalores y autovectores. (Esto lo veremos más adelante en la Unidad 8: Aplicaciones de la diagonalización)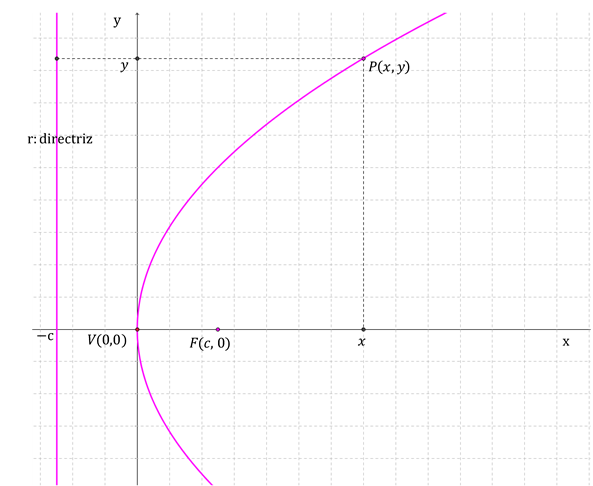 Para el esquema que realizamos, las coordenadas del vértice son , las del foco y la recta directriz está dada por . Las coordenadas de un punto genérico que pertenece a la directriz son .Ahora con estos datos vamos a deducir la ecuación. Por definición:Distancia entre un punto P y la directriz:
Para el esquema que realizamos, las coordenadas del vértice son , las del foco y la recta directriz está dada por . Las coordenadas de un punto genérico que pertenece a la directriz son .Ahora con estos datos vamos a deducir la ecuación. Por definición:Distancia entre un punto P y la directriz: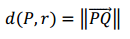 Distancia entre un punto P y el foco:
Distancia entre un punto P y el foco: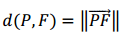 Las igualamos según lo establece la definición:
Las igualamos según lo establece la definición: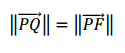 Donde los vectores y sus módulos son:
Donde los vectores y sus módulos son: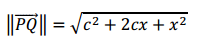
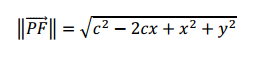 Ahora sustituyendo y operando llegamos a:Que es la ecuación canónica de la parábola con y eje focal (eje ).Donde si,Las ramas de la parábola apuntan hacia la derechaLas ramas de la parábola apuntan hacia la izquierdaAnálogamente a lo desarrollado para una parábola con eje focal horizontal, se puede hacer la deducción para las parábolas con eje focal vertical. Si permutamos variables sobre la expresión canónica tenemos la expresión canónica de la parábola vertical:Ecuación canónica de la parábola con y eje focal (eje ).Donde si,Las ramas de la parábola apuntan hacia la arribaLas ramas de la parábola apuntan hacia la abajoCoordenadas del foco:Ecuación de la directriz
Ahora sustituyendo y operando llegamos a:Que es la ecuación canónica de la parábola con y eje focal (eje ).Donde si,Las ramas de la parábola apuntan hacia la derechaLas ramas de la parábola apuntan hacia la izquierdaAnálogamente a lo desarrollado para una parábola con eje focal horizontal, se puede hacer la deducción para las parábolas con eje focal vertical. Si permutamos variables sobre la expresión canónica tenemos la expresión canónica de la parábola vertical:Ecuación canónica de la parábola con y eje focal (eje ).Donde si,Las ramas de la parábola apuntan hacia la arribaLas ramas de la parábola apuntan hacia la abajoCoordenadas del foco:Ecuación de la directriz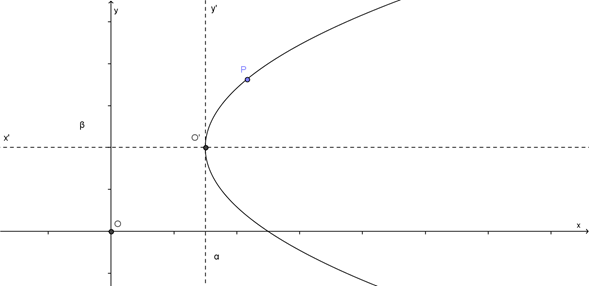 ¿Cómo sería la ecuación de la parábola en el sistema de referencia ? No sabemos responder esto por el momento. Pero si armamos un nuevo sistema cuyo centro coincida con , la ecuación canónica en este nuevo sistema sería:Debemos realizar una traslación de ejes para poder tener la ecuación escrita en el sistema
¿Cómo sería la ecuación de la parábola en el sistema de referencia ? No sabemos responder esto por el momento. Pero si armamos un nuevo sistema cuyo centro coincida con , la ecuación canónica en este nuevo sistema sería:Debemos realizar una traslación de ejes para poder tener la ecuación escrita en el sistema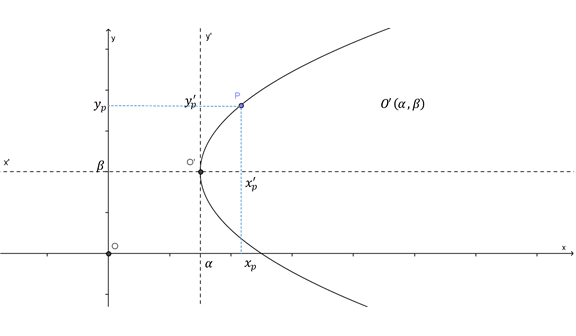 ¿Qué coordenadas tiene el punto respecto de cada sistema?El punto es el mismo pero estamos modificando el sistema de referencia:
¿Qué coordenadas tiene el punto respecto de cada sistema?El punto es el mismo pero estamos modificando el sistema de referencia: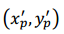
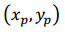
 El valor absoluto de es la distancia del vértice al foco.El vértice está sobre el eje focal y a la misma distancia del foco que de la directriz:Eje focal: ejeComo el eje es horizontal la ecuación tiene la forma:Falta calcular el valor absoluto de .Como el foco está a la izquierda del vértice entonces .Entonces queda:
El valor absoluto de es la distancia del vértice al foco.El vértice está sobre el eje focal y a la misma distancia del foco que de la directriz:Eje focal: ejeComo el eje es horizontal la ecuación tiene la forma:Falta calcular el valor absoluto de .Como el foco está a la izquierda del vértice entonces .Entonces queda: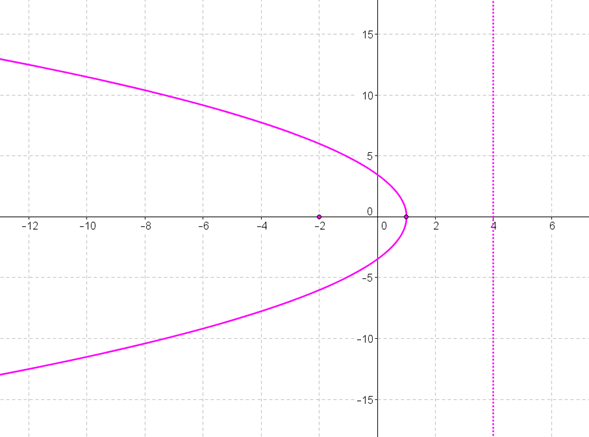
Comentarios
Publicar un comentario