Funciones Polinomiales Y Racionales

Funciones Cuadráticas 

En matemáticas, una función cuadrática es una variable de una función polinómica definida por:

${\displaystyle y=ax^{2}+bx+c\,}$

con ${\displaystyle a\neq 0}$.¹​ También se da el caso que se le llame Trinomio cuadrado perfecto.²​ También se denomina función cuadrática a funciones definidas por polinomios cuadráticos de más de una variable, por ejemplo:

${\displaystyle f(x,y)=Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F}$

En este caso el conjunto de puntos que resultan al igualar el polinomio a cero representan lugares geométricos que siempre es posible reducir a una de las formas:

${\displaystyle \left({\frac {x}{a}}\right)^{2}\pm \left({\frac {y}{b}}\right)^{2}=c^{2},\qquad \left({\frac {x}{a}}\right)^{2}\pm {\frac {y}{b}}=c}$

Que corresponden a tres tipos de secciones cónicas (elipse, hipérbola y parábola).

Funciones cuadráticas de una variable

Las gráficas de estas funciones corresponden a parábolas verticales (eje de simetría paralelo al eje de las ordenadas), con la particularidad de que cuando a>0, el vértice de la parábola se encuentra en la parte inferior de la misma, siendo un mínimo (es decir, la parábola se abre "hacia arriba"), y cuando a<0 el vértice se encuentra en la parte superior, siendo un máximo (es decir, la parábola se abre "hacia abajo").

El estudio de las funciones cuadráticas tiene numerosas aplicaciones en campos muy diversos, por ejemplo la caída libre o el tiro parabólico.

La derivada de una función cuadrática es una función lineal y su integral indefinida es una familia de funciones cúbicas.

Raíces

Las raíces (o ceros) de una función cuadrática, como en toda función, son los valores de x, para los cuales ${\displaystyle ax^{2}+bx+c=0\ }$. Son denotadas habitualmente como: ${\displaystyle x_{1}}$ y ${\displaystyle x_{2}}$, dependiendo del valor del discriminante Δ definido como ${\displaystyle \Delta =b^{2}-4ac\ }$.

• Dos soluciones reales y diferentes si el discriminante es positivo, ${\displaystyle \Delta >0}$:

${\displaystyle x_{1}={\frac {-b+{\sqrt {\Delta }}}{2a}}}$

${\displaystyle x_{2}={\frac {-b-{\sqrt {\Delta }}}{2a}}}$

• Corta la parábola al eje X en dos puntos diferentes.

• Una solución real(o solución doble) si el discriminante es cero, ${\displaystyle \Delta =0}$:

${\displaystyle x_{1}=x_{2}=-{\frac {b}{2a}}}$

• La parábola es tangente al eje X.

• La parábola no corta al eje X.

• El único caso restante es que el discriminante sea negativo, ${\displaystyle \Delta <0}$.

En tal caso, las raíces no son reales, sino que son dos números complejos conjugados:

${\displaystyle x_{1}={\frac {-b}{2a}}+i{\frac {\sqrt {-\Delta }}{2a}}}$

${\displaystyle x_{2}={\frac {-b}{2a}}-i{\frac {\sqrt {-\Delta }}{2a}}}$

Representación analítica

Hay tres formas de escribir una función cuadrática, aplicables según el uso que se le quiera dar a la función, un estudio analítico de la función o de la ecuación cuadrática, una interpretación o construcción geométrica de la parábola, etc.

Forma desarrollada o polinómica

La forma desarrollada de una función cuadrática (o forma estándar) corresponde a la del polinomio de segundo grado, escrito como:

${\displaystyle f(x)=ax^{2}+bx+c\,}$

con ${\displaystyle a\neq 0}$.

Forma factorizada

Toda función cuadrática se puede escribir en forma factorizada en función de sus raíces como:

${\displaystyle f(x)=a(x-x_{1})(x-x_{2})\,}$

siendo a el coeficiente principal de la función, y ${\displaystyle x_{1}}$ y ${\displaystyle x_{2}}$ las raíces de ${\displaystyle f(x)}$. En el caso de que el discriminante Δ sea igual a 0 entonces ${\displaystyle x_{1}=x_{2}}$ por lo que la factorización adquiere la forma:

${\displaystyle f(x)=a(x-x_{1})^{2}\,}$

En este caso a ${\displaystyle x_{1}}$ se la denomina raíz doble, ya que su orden de multiplicidad es 2. Si el discriminante es negativo, las soluciones son complejas, no cabe la factorización.

Representación gráfica

Intersección con el eje y

La función corta el eje y en el punto y = f(0), es decir, la parábola corta el eje y cuando x vale cero (0):

${\displaystyle y=f(0)=a\cdot 0^{2}+b\cdot 0+c\,}$

lo que resulta:

${\displaystyle y=f(0)=c\,}$

la función corta el eje y en el punto (0, c), siendo c el término independiente de la función.

A este punto de la función también se lo conoce con Ordenada al Origen, ya que se da en los términos.

Intersección con el eje x

La función corta al eje x cuando y vale 0, dada la función

${\displaystyle y=ax^{2}+bx+c\,}$

es decir:

${\displaystyle y=0\quad \longmapsto \quad ax^{2}+bx+c=0\,}$

las distintas soluciones de esta ecuación de segundo grado, son los casos de corte con el eje x, que se obtienen, como es sabido, por la expresión:

${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}$.

Si la función no corta al eje x, la fórmula anterior no tiene solución real. Puede ocurrir que no tenga intersecciones con el eje x, por ejemplo ${\displaystyle y=x^{2}+2}$.

Extremo

En principio, en matemáticas se nombra como extremo tanto al máximo como al mínimo, por ejemplo en el conjunto S = {1,5,9, 13, 17} el mínimo es 1 y el máximo 17, y los extremos son 1 y 17. Para calcular el extremo de una función cuadrática, se puede usar un teorema, abordable en álgebra elemental, apoyándose en el comportamiento de una suma de un cuadrado de una variable con un número real cualquiera.⁵​

Teorema fundamental del trinomio cuadrático

El trinomio cuadrático real

${\displaystyle y=ax^{2}+bx+c}$ ̝

tiene un valor extremo que lo consigue cuando

${\displaystyle x={\frac {-b}{2a}}}$

Funciones De Grado Superior

Para hallar ceros de las funciones polinomiales de tercer y cuarto grados existen soluciones algebraicas; sin embargo, son muy complicadas y nada practicas. El frances Evaristo Galvin demostro en 1920 que no existe formula algebraica para resolver una ecuacion polinomial de la forma:

Por lo que se intentaran hallar los ceros por tanteos, pero siempre bajo un orden y utilizando un conjunto de herramientas y propiedades de los polinomios que nos permita proceder de una manera razonable y con precision utilizando la teoria de las ecuaciones para hallar los ceros de polinomios de grado superior (n>2) cuyos coeficientes sean numeros reales y racionales.

Función Polinomial

Si x=a es una raíz de la ecuación P(x)=0, donde P(x) es un polinomio, entonces (x/a) es un factor de P(x).

Competencias Desarrolladas y Referencias

Toda ecuación racional entera f(x)=0, de grado n>0 tiene al menos una raíz. Si un numero complejo a+bi, es una raíz de una ecuación polinomial racional entera, f(x)=0 de coeficientes reales, entonces su complejo conjugado a-bi también es una raíz de f(x)=0. Un polinomio f(x) de grado n tiene exactamente n raíces o ceros no necesariamente diferentes.

Para este teorema tomaremos como base:

Las raíces de f(x)=0 pueden ser reales o complejas y se pueden repetir, como lo hemos señalado. Una raíz de multiplicidad k se cuenta n veces.

La forma factorizada de un polinomio con coeficientes reales nos permite construir una ecuación si conocemos sus races.

4.Escucha, interpreta y emite mensajes pertinentes en distintos contextos mediante la utilizacion de medios, codigos y herramientas apropiadas.

5. Desarrolla innovaciones y propone soluciones a partir de métodos establecidos.

Encuentra el residuo que resulta al dividir el polinomio f(x)=x2-7x+15 por x-4.

Una función cuadrática es aquella que tiene la forma, o puede ser llevada a la forma:

y = f (x) = ax2 + bx + c , con a ≠ 0 , a,b,c∈ y su dominio es R

1. El gráfico de una función lineal es siempre una línea recta.

2. El coeficiente a es la pendiente de la recta y=ax+b. Cuando a>0, la función lineal es creciente, y cuando a <0, la función lineal es decreciente.

3. El dominio y el recorrido de una función lineal es R.

4. La función lineal y = f(x) = ax + b , con a ≠ 0 es inyectiva (y sobre), por lo tanto, tiene inversa. Su inversa es también una

función lineal.

Teorema fundamental del álgebra

Los ceros de una funcion polinomial

Si un polinomio P(x) se divide entre x-a hasta obtener un residuo en el que no aparece la variable x, el residuo resultante es igual a P(a).

Si dividimos P(x) entre x-a y designamos por Q(x) el cociente y por r el residuo, entonces P(x)=Q(x)(x-a) + r.

Como la igualdad anterior es valida para todo x ∈R, lo sera para x=a, luego:

Encuentra la expresión del polinomio f(x) de grado 3 cuyos ceros sean 2,4 y -5 tal que f(3)=-24

Integrantes

Jenny Carolina López Zamarrón. 1668183 #24

Lina Alondra Mata Padrón. 1657739 #27

Las funciones polinomiales y su representación gráfica, tienen gran importancia en la Matemática. Estas funciones son modelos que describen relaciones entre dos variables que intervienen en diversos problemas y/o fenómenos que provienen del mundo real.

La función polinomial se llama si porque generalmente su expresión algebraica es un polinomio; su forma general es:

En esta actividad integradora se mostrara lo que es una función polinomial, sus diversos tipos y como resolverlas.

Gráfica de y = ax + b , a < 0

Una función cúbica es aquella que tiene la forma, o puede ser llevada a la forma: y = f (x) = ax3 + bx2 + cx + d , con a ≠ 0 , a,b,c,d ∈ y su dominio es R.

1. El gráfico de una función cuadrática es una parábola.

2. La gráfica de y = f(x) = ax2 + bx + c intercepta al eje Y en el punto (0,c) La gráfica de y = f(x) = ax2 + bx + c intercepta al eje X cuando Δ = b2 − 4ac> 0 , y en tal caso, las abscisas de los puntos de intersección son las raíces de la ecuación ax2 + bx + c = 0.

3. Su gráfica es una parábola cuyo vértice es el punto

4. La recta vertical es una recta eje de simetría de su gráfico.

5. Si a>0 la parábola se abre hacia arriba, y si a<0 se abre hacia abajo.

Al multiplicar (x-2) (x-4) (x+5) resulta.

El teorema del residuo nos permite hallar el valor de un polinomio f(x) mediante la división de este entre un binomio pero hay una manera mas rápida de resolverlo que es mediante la división sintética.

1. La gráfica de y = f (x) intercepta al eje Y en el punto (0,c)

2. La gráfica de y = f (x) intercepta al eje X en los puntos cuyas abscisas son las raíces de la

ecuación a xn + + a1x + a0 = 0

3. Las funciones polinomiales son funciones continuas.

Los ceros de una función polinomial

Competencias genéricas

Gráficas

Para hallar los ceros de una función polinomial se

necesita que n>2 y los coeficientes sean números reales

y racionales.

Los ceros de una función polinomial definida por la ecuación y=f(x) son aquellos valores de x que son la solución de la ecuación f(x)=0. Si los ceros son números reales, entonces son las intersecciones con el eje x de su gráfica.

Los 3 teoremas importantes para hallar los ceros es el teorema del residuo, del factor y la división sintética siendo esta última la mas sencilla.

Si se tiene que encontrar el residuo de un polinomio de 3 grados y nos den los 3 valores de x utilizar el teorema

fundamental del álgebra.

Teorema del residuo

Función Lineal

f(x)=c

Función Cuadrática

Una función constante es aquella que tiene la forma

y=f(x)=c, donde c es un número real fijo.

El dominio de una función constante es R, y su recorrido es {c}. Su gráfica es una recta paralela (o coincidente) al eje X.

Teorema del factor

Gráfica

Función Constante

Para determinar si x+3 es un factor de P(x)=x3+x2-7x-3 bastara con determinar si x=-3 es raíz de dicha ecuación. Si f(-3)=0, entonces x+3 si es un factor de P(x)

Sustitución de valores

Gráfica de y = ax + b , a > 0

-Maneja las tecnologías de la información y la comunicación como herramienta para el acceso a la información y su transformación en conocimiento, así como para el aprendizaje y trabajo colaborativo con técnicas de vanguardia que le permitan su participación constructiva en la sociedad.

-Utiliza los métodos y técnicas de investigación tradicionales y de vanguardia para el desarrollo de su trabajo académico, el ejercicio de su profesión y la generación de conocimientos.

División Sintética

Propiedades

Referencias

Conclusión

Una función lineal es aquella que tiene la forma, o

puede ser llevada a la forma: y = f (x) = ax + b , con

a ≠ 0 , a,b∈ R

Función Racional 

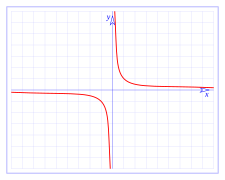
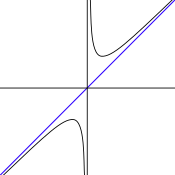
En matemáticas, una función racional de una variable es una función que puede ser expresada de la forma:

${\displaystyle f(x)={\frac {P(x)}{Q(x)}}}$

donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo, esta fracción es irreducible, es decir que las ecuaciones P(x) = 0 y Q(x) = 0 carecen de raíces comunes. Esta definición puede extenderse a un número finito pero arbitrario de variables, usando polinomios de varias variables.

La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.

Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados de otras funciones más complejas, ya que son computacionalmente simples de calcular como los polinomios, pero permiten expresar una mayor variedad de comportamientos.

Ejemplos[editar]

Función homográfica:

${\displaystyle f(x)={\frac {ax+b}{cx+d}}}$

si el denominador es distinto de cero, y si ad ≠ bc, la curva correspondiente es una hipérbola equilátera.¹​

Propiedades[editar]

• Toda función racional es de clase ${\displaystyle C^{\infty }}$ en un dominio que no incluya las raíces del polinomio Q(x).
• Todas las funciones racionales en las que el grado de Q sea mayor o igual que el grado de P tienen asíntotas (verticales, horizontales u oblicuas).
• Todas las funciones racionales cuyos coeficientes pertenecen a un cuerpo forman un cuerpo que incluye al cuerpo base como subcuerpo. El cuerpo de funciones racionales forma un subcuerpo del cuerpo de series de potencias formales.

Integración de funciones racionales[editar]

Dada una función racional:

${\displaystyle f(x)={\frac {P(x)}{Q(x)}},\qquad P(x),Q(x)\in \mathbb {R} [x]}$

Si el denominador es un polinómico mónico ${\displaystyle \scriptstyle Q(x)}$ con k raíces diferentes, entonces admitirá la siguiente factorización en términos de polinomio irreducibles:

${\displaystyle {\begin{cases}Q(x)=(x-r_{1})^{m_{1}}(x-r_{2})^{m_{2}}\dots (x-r_{k})^{m_{k}}(x^{2}+s_{1}x+t_{1})^{n_{1}}\dots (x^{2}+s_{l}x+t_{l})^{n_{l}}\\k,l,m_{i},n_{j}\in \mathbb {N} ,\ r_{p},s_{p},t_{p}\in \mathbb {R} \end{cases}}}$

Si ${\displaystyle \scriptstyle {\mbox{gr}}(P)<{\mbox{gr}}(Q)}$ entonces la función racional puede escribirse como combinación lineal de fracciones racionales de las formas:

${\displaystyle {\begin{matrix}f_{1}(x)={\cfrac {1}{(x-r_{i})}}&f_{2}(x)={\cfrac {1}{(x-r_{i})^{u}}}\\f_{3}(x)={\cfrac {1}{x^{2}+a^{2}}}&f_{4}(x)={\cfrac {1}{(x^{2}+a^{2})^{v}}}\\f_{5}(x)={\cfrac {x}{x^{2}+a^{2}}}&f_{6}(x)={\cfrac {x}{(x^{2}+a^{2})^{w}}}\end{matrix}}}$

Por lo que la integral de la función ${\displaystyle \scriptstyle f_{i}(x)}$ es una combinación lineal de funciones de la forma ${\displaystyle \scriptstyle F_{i}(x)}$ :

${\displaystyle {\begin{matrix}F_{1}(x)=\ln(x-r_{i})&F_{2}(x)={\cfrac {1-u}{(x-r_{i})^{u-1}}}\\F_{3}(x)={\cfrac {1}{a}}\arctan {\cfrac {x}{a}}&F_{4}(x)={\cfrac {1}{2a^{2}}}\left({\cfrac {x}{(v-1)(x^{2}+a^{2})^{v-1}}}+{\cfrac {2v-3}{v-1}}\int {\cfrac {dx}{(x^{2}+a^{2})^{v-1}}}\right)\\F_{5}(x)={\cfrac {1}{2}}\ln(x^{2}+a^{2})&F_{6}(x)={\cfrac {-1}{2(w-1)(x^{2}+a^{2})^{w-1}}}\end{matrix}}}$

Obsérvese que lo anterior implica que las funciones racionales constituyen un cuerpo algebraico que es cerrado bajo la derivación, pero no bajo la integración.

Asíntota

Ir a la navegaciónIr a la búsqueda

Gráfica de dos hipérbolas y sus asíntotas en el plano cartesiano.

En matemática, se le llama asíntota de la gráfica de una función a una recta a la que se aproxima continuamente la gráfica de tal función;¹​ es decir que la distancia entre las dos tiende a ser cero (0), a medida que se extienden indefinidamente.
O que ambas presentan un comportamiento asintótico. Generalmente, las funciones racionales tienen comportamiento asintótico.

Las asíntotas ayudan a la representación de curvas, proporcionan un soporte estructural e indican su comportamiento a largo plazo. En tanto que líneas rectas, la ecuación de una asíntota es simplemente la de una recta, y su expresión analítica dependerá de la elección del sistema de referencias (y = m•x + b en coordenadas cartesianas).

Si bien suelen representarse en un mismo sistema de coordenadas, las asíntotas no forman parte de la expresión analítica de la función, por lo que -en numerosos ejemplos- no están incluidas explícitamente dentro de la gráfica, o bien se las indica con una línea punteada.
En muchos casos, las asíntotas coinciden con los ejes de coordenadas, es decir que sus ecuaciones en coordenadas cartesianas serán: x = 0, y = 0.

Se distinguen tres tipos:

• Asíntotas verticales: rectas perpendiculares al eje de las abscisas, de ecuación x = constante.
• Asíntotas horizontales: rectas perpendiculares al eje de las ordenadas, de ecuación y = constante.
• Asíntotas oblicuas: si no son paralelas o perpendiculares a los ejes, de ecuación y = m•x + b.

Las ramas de la función tienen asíntotas.

Los ejes son las asíntotas.

Las ramas de la función tienen asíntotas.